Ondalık Gösterimlerin Üslü Gösterimi Test Soruları 8. Sınıf

Soru 1
Aşağıdaki sayılardan hangisinin üslü gösterimi 2,76 . 10⁻³’tür?

A) 0,00276
B) 0,0276
C) 2760
D) 276 10⁻³, ondalık noktanın sola doğru 3 basamak kaydırılacağını gösterir.
2,76 . 10⁻³ = 0,00276
Doğru Cevap AABCD

Soru 2
4.10² + 1.10⁰ + 3.10^-1 + 5.10^-3
Yukarıda çözümlenmiş hali verilen ondalık gösterim aşağıdakilerden hangisidir?

A) 41,35
B) 41,305
C) 401,305
D) 401,35 Verilen sayıları ilgili basamaklara yazarak sayıyı bulalım.
4.10² + 1.10⁰ + 3.10^-1 + 5.10^-3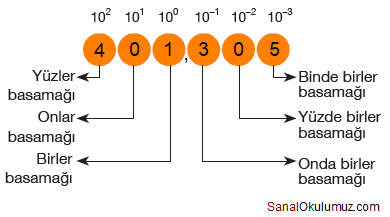
Doğru Cevap CABCD

Soru 3
I. 24,2 . 10^-23 = 242 . 10^-22
II. 0,000000000000542 = 542 . 10^-15
III. 0,0351 . 10¹⁶ = 351 . 10¹²
Yukarıda verilen eşitliklerden hangileri doğrudur?

A) Yalnız I     B) I ve II     C) I ve III     D) II ve III I. Yanlış. Çünkü 24,2 . 10^-23 ≠ 242 . 10^-22.
24,2 . 10^-23 = 242 . 10^-24 olmalıdır.
II. Doğru. 542 sayısının en sağından virgülün olduğu yere kadar 15 basamak vardır.
III. Doğru. Virgülü 4 basamak sağa kaydırdığımızda 351 sayısı elde edilir ve 10’un üssü 4 azalır.
Doğru Cevap DABCD

Soru 4
x . 10³² = 3,9 . 10²⁷ eşitliğini sağlayan x değeri kaçtır?

A) 0,0039
B) 0,00039
C) 0,000039
D) 0,0000039 Eşitliğin her iki tarafını 10³²'ye bölerek x’i yalnız bırakalım:
x . 10³²10³² = 3,9.10²⁷10³²
x = 3,9 . 10^{27 − 32}
x = 3,9 . 10⁻⁵
x = 0,000039
Doğru Cevap CABCD

Soru 5
0,000001056 . 10^x sayısının değeri 1000’den büyüktür. Buna göre x yerine yazılabilecek en küçük doğal sayı kaçtır?

A) 8     B) 9     C) −9     D) −10 Verilen ondalık sayının 1000’den büyük olabilmesi için sayının tamamının virgülden kurtulması gerekir. Bunun için, virgülün sağa doğru 9 basamak kaydırılması gerekir.
0,000001056 . 10⁹ = 1056
Böylece sayımız 1000’den büyük olur.
Bu durumda x en az 9 olacaktır.
Doğru Cevap BABCD

Soru 6
7 . 10³ + 3 . 10² + 4 + 5 . 10⁻¹ + 2 . 10⁻³
Yukarıda çözümlemesi verilen sayının onda birler basamağı ile binler basamağındaki rakamın çarpımı kaçtır?

A) 35     B) 36     C) 40     D) 42 İlk önce sayımızı bulalım.
7 . 10³ = 7000 (Binler basamağı 7)
3 . 10² = 300 (Yüzler basamağı 3)
4 (Birler basamağı 4)
5 . 10⁻¹ = 0,5 (Onda Birler basamağı 5)
2 . 10⁻³ = 0,002 (Binde birler basamağı 2)
Sayımız;
7304,502
Onda birler basamağı ile binler basamağındaki rakamın çarpımı;
5 . 7 = 35
Doğru Cevap AABCD

Soru 7
Aşağıdaki eşitliklerden hangisi doğrudur?

A) 3856 . 10¹² = 38,56 . 10¹³
B) 385,6 . 10¹⁴ = 38,56 . 10¹³
C) 38,56 . 10¹⁵ = 3,856 . 10¹⁴
D) 3,856 . 10¹⁰ = 385,6 . 10⁸ A) Yanlış. 3856 . 10¹² = 38,56 × 10¹⁴ olmalı.
B) Yanlış. 385,6 . 10¹⁴ = 38,56 . 10¹⁵ olmalı.
C) Yanlış. 38,56 . 10¹⁵ = 3,856 . 10¹⁶ olmalı.
D) Doğru.
Doğru Cevap DABCD

Soru 8
0,072 . 10⁻¹⁰ = 7,2 . 10^a işleminde a sayısı kaçtır?

A) −10     B) −12     C) −13     D) −14 Eşitliğin sol tarafındaki 0,072 ondalık sayısını 7,2 ondalık sayısına dönüştürürsek a’yı rahatlıkla buluruz.
0,072 . 10⁻¹⁰ = 7,2 . 10⁻¹² olur.
Virgülü 2 basamak sağa kaydırdığımız için üssü 2 azalttık.
Şimdi denklemi yeniden yazalım.
7,2 . 10⁻¹² = 7,2 . 10^a
Ondalık sayılarımız aynı olduğu için üslü sayılarımızda aynı olmalıdır. Bu durumda;
10⁻¹² = 10^a
a = −12
Doğru Cevap BABCD

Soru 9
6 . 10² + 8 . 10¹ + 4 . 10⁰ + 5 . 10⁻¹ + 2 . 10⁻² + 3 . 10⁻³
Yukarıda çözümlemesi verilen sayının, yüzde birler basamağı ile yüzler basamağındaki rakamların çarpımı kaçtır?

A) 30     B) 18     C) 12     D) 10 Yüzler basamağı (6 . 10²) : 6
Yüzde birler basamağı (2 . 10⁻²) : 2
Çarpımı: 6 . 2 = 12
Doğru Cevap CABCD

Soru 10
306,547 = 3 . 10² + 0 . 10¹ + 6 . 10⁰ + a . 10⁻¹ + 4 . 10⁻² + b . 10⁻³
Yukarıdaki eşitliğe göre a + b = ?

A) 12     B) 13     C) 14     D) 15 a . 10⁻¹ onda birler basamağıdır ve bu basamakta 5 rakamı bulunuyor.
a = 5
b . 10⁻³ binde birler basamağıdır ve bu basamakta 7 rakamı bulunuyor.
b = 7
a + b = 5 + 7 = 12
Doğru Cevap AABCD