9. Sınıf İki Kümenin Kartezyen Çarpımı ve Sıralı İkili

İKİ KÜMENİN KARTEZYEN ÇARPIMI
SIRALI İKİLİ
a ve b elemanlarının belli bir öncelik sırasına göre (a, b) biçiminde tek bir eleman olarak yazılmasına sıralı ikili ya da kısaca ikili denir.

(a, b) sıralı ikilisinde a ya birinci bileşen, b ye de ikinci bileşen denir.

ÖNEMLİ !
Sıralı ikilide bileşenlerin sırası önemlidir. Bileşenlerin sırası değişirse başka bir ikili elde edilir.

a ≠ b ⇔ (a, b) ≠ (b, a) dır.
(a, b) = (x, y) ⇔ a = x ve b = y dir.

İki Kümenin Kartezyen Çarpımı
A ve B boş olmayan iki küme olsun. Birinci bileşeni A dan, ikinci bileşeni B den alınarak oluşturulan bütün ikililerin kümesine A ile B kümesinin kartezyen çarpımı denir ve A X B şeklinde gösterilir.

A X B = {(a, b) | a ∈ A ve b ∈ B} dir.

A ≠ B için A X B ≠ B X A dır. (kartezyen çarpımın değişme özelliği yoktur.)

A X B X C = (A X B) X C = A X (B X C) (Kartezyen çarpımın birleşme özelliği vardır.)

A X A = A²

A X A X A = A³ tür.

s(A X B) = s(B X A) = s(A).s(B) dir.

A X (B ∪ C) = (A X B) ∪ (A X C)

A X (A ∩ C) = (A X B) ∩ (A X C)

A X (B – C) = (A X B) – (A X C) (Kartezyen çarpımın birleşim, kesişim ve fark işlemi üzerine dağılma özelliği vardır.)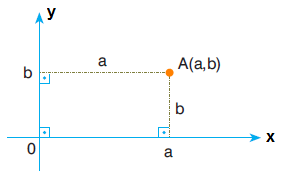

A X B kartezyen çarpımının grafiği;
A nın elemanları 0x ekseni (yatay eksen) üzerinden, B nin elemanları 0y ekseni (düşey eksen) üzerinden alınarak elde edilen (a, b) ikilileri koordinat düzleminde gösterilir.