9. Sınıf Kümelerde İşlemler Konu Anlatımı

KÜMELERDE İŞLEMLER
a) Birleşim İşlemi
A kümesi ile B kümesinin bütün elemanlarından oluşan kümeye, bu iki kümenin birleşimi denir.
A ∪ B şeklinde gösterilir. A ∪ B kümesi aşağıdaki şekildeki taralı bölgedir.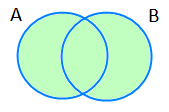

Kümelerde birleşim ile ilgili özellikler;
A ∪ A = A (Tek kuvvet özelliği)

A ∪ Ø = A

A ∪ E = E

A ∪ B = B ∪ A (Değişme özelliği)

(A ∪ B) ∪ C = A ∪ (B ∪ C) (Birleşme özelliği)

A ∪ B = Ø ise A = Ø ve B = Ø dir.

A ⊂ B ise A ∪ B = B dir.

b) Kesişim İşlemi
A kümesi ile B kümesinin ortak elemanlarından oluşan kümeye, bu iki kümenin kesişimi denir.
A ∩ B şeklinde gösterilir. A ∩ B kümesi taralı bölgedir.

Kümelerde kesişim ile ilgili özellikler;

A ∩ A = A dır. (Tek kuvvet özelliği)

A ∩ Ø = Ø ∩ A = Ø

A ∩ E = E ∩ A = A

A ∩ B = B ∩ A (Değişme özelliği)

(A ∩ B) ∩ C = A ∩ (B ∩ C) (Birleşme özelliği)

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) (Birleşimin kesişim üzerine dağılma özelliği)

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) (Kesişimin birleşim üzerine dağılma özelliği)

A ⊂ B ? A ∩ B = A

A ? Ø ve B ? Ø olmak üzere,
A ∩ B = Ø ise A ile B kümelerine ayrık kümeler denir.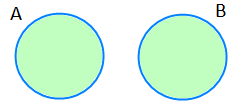

A ile B ayrık kümeler

s(A ∪ B) = s(A) + s(B) – s(A ∩ B)

s(A ∪ B ∪ C) = s(A) + s(B) + s(C) – s(A ∩ B) – s(A ∩ C) – s(B ∩ C) + s(A ∩ B ∩ C)

c) Tümleme İşlemi
E, evrensel küme ve A ⊂ E olsun.
Evrensel kümede olan fakat A kümesinde olmayan bütün elemanların oluşturduğu kümeye A nın tümleyeni denir ve A^ı ile gösterilir.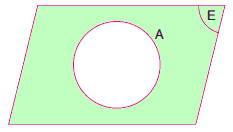

Taralı bölge A kümesinin tümleyenidir.

A ∩ A^ı = Ø

A ∪ A^ı = E

Ø^ı = E, E^ı = Ø

(A^ı)^ı = A

s(A) + s(A^ı) = s(E)

A ⊂ B ? B^ı ⊂ A^ı

(A ∪ B)^ı = A^ı ∩ B^ı (De Morgan kuralı)

(A ∩ B)^ı = A^ı ∪ B^ı (De Morgan kuralı)

d) Fark İşlemi
A ve B herhangi iki küme olsun. A kümesinin elemanları içinden varsa B kümesinin elemanları çıkarılarak elde edilen kümeye “A fark B” kümesi denir ve A \ B ya da A – B şeklinde gösterilir.

A – A = Ø

E – A = A^ı

A – B = A ∩ B^ı

A ? B ise A – B ? B – A

A – Ø = A, Ø – A = Ø

(A – B) ∪ B = A ∪ B

(A – B) – C = A – (B ∪ C)

KÜMELERDEKİ İŞLEMLERLE PROBLEM ÇÖZÜMÜ
Yukarıdaki venn şemasında Almanca bilenlerin kümesi A, Fransızca bilenlerin kümesi F ile gösterilmiştir.

Almanca bilenlerin sayısı s(A) = x + y

Fransızca bilenlerin sayısı s(F) = y + z

Almanca bilmeyenlerin sayısı s(A^ı) = t + z

Fransızca bilmeyenlerin sayısı s(F^ı) = x + t

Almanca ve Fransızca bilenlerin sayısı s(A ∩ F) = y

Almanca veya Fransızca bilenlerin sayısı s(A ∪ F) = x+y+z

Almanca bilip, Fransızca bilmeyenlerin sayısı s(A – F) = x

Fransızca bilip, Almanca bilmeyenlerin sayısı; s(F – A) = z

Yalnız bir dil bilenlerin sayısı; s(A – F) + s(F – A) = x + z

Bu dillerin hiçbirini bilmeyenlerin sayısı, s(A ∪ F)^ı = t

Bu iki dilden en az birini bilenlerin sayısı; s(A∪F)= x+y+z

Bu iki dilden en çok birini bilenlerin sayısı; s(A ∩ F)^ı = x+z+t dir.

Benzer İçerikler

9. Sınıf Matematik Kümelerde Fark İşlemi Konu Anlatımı
9. Sınıf Matematik Kümelerde Temel Kavramlar Konu Anlatımı
9. Sınıf İki Kümenin Kartezyen Çarpımı ve Sıralı İkili Konu Özeti
9. Sınıf Matematik Kümeler Çözümlü Test Soruları
9. Sınıf Matematik Kümelerde İşlemler Çözümlü Test Soruları

Hızlı Erişim