- Cemre Solmaz Gayet güzel bir uygulama sorular yeterince iyi konu anlatımından çalışıyorum.
- İsimsiz Gerçekten çok güzel bir sayfa yardımlarınız için teşekkür ederim.
- Matematik Projesi Size tek söyleyeceğim şey bir matematik projesi aldım çember ile ilgili ve bu sayfa bana yardımcı oldu süper bir sayfa ellerinize sağlık.
- Mimar Sinan Çözümlü sorular daha fazla olmalı.
- Yasemin Çok açık ve net bir şekilde anlatılmış çok güzel.
- Ali Çoook teşekkür ederim sizin sayenizde sınavdan yüksek not alacağım inşallah.
- Cemre Güzel ve net ayrıca genelde sınavları buradan soruyorlar.
- Sadece Matematik Harika, bu siteye bayılıyorum. Unuttuğum, anlamadığım, tekrar etmek istediğim veya önceden çalışmak istediğim konuları ŞIP diye anlıyorum. Kafamdakileri pekiştirmek istediğimde de işe yarayan yardımcılarımdan. Teşekkürler.
- Hasan Bence çok güzel size burada çalışmanızı tavsiye ederim.
- Teşekkürler Çok başarılı bir konu anlatım sitesi.
7. Sınıf Matematik Çember ve Daire Konu Anlatımı
ÇEMBER VE DAİRENİN ÖZELLİKLERİ
Çember: Sabit bir noktaya eşit uzaklıkta noktaların kümesine çember denir.
Sabit noktaya, çemberin merkezi, bu noktayla çember üzerindeki bir noktayı birleştiren doğru parçasına çemberin yarıçapı denir.
Çemberin içinde kalan noktaların oluşturduğu bölge çemberin iç bölgesi, dışında kalan noktaların oluşturduğu bölge çemberin dış bölgesidir.
DAİRE : Çember ile çemberin iç bölgesinin birleşimine daire denir.
Çember kapalı bir eğri, daire ise bir düzlem parçasıdır.
Çemberin yalnızca uzunluğu, dairenin ise alanı ve çavre uzunluğu vardır.
KESEN: Bir çemberin üzerindeki iki noktadan geçen doğruya kesen denir. 
KİRİŞ: Kesenin çemberi kestiği noktalar arasında kalan parçasına kiriş denir. 
Merkezden geçen kirişe çap denir. Çap aynı zamanda bir çemberin en uzun kirişidir.
Bir çemberde merkezden eşit uzaklıktaki kirişlerin uzunlukları eşittir. Merkeze yakın kiriş daha uzundur.
TEĞET: Çemberi bir noktada kesen doğruya teğet denir. Aşağıdaki şekilde d doğrusu, K noktasından çembere teğet geçmektedir.
ÇEMBERDE YAYLAR
Çember üzerindeki iki nokta arasında kalan parçaya çember parçası, çember yayı veya kısaca yay denir. 
Bir çemberde eşit uzunluktaki kirişleri gören yayların uzunlukları eşittir. 
MİNÖR VE MAJÖR YAY (Büyük ve Küçük Yay)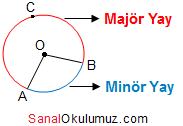
Merkez açının kenarlarının çemberi veya daireyi kestiği noktaların arasındaki büyük çember yayına majör (büyük) çember yayı, küçük çember yayına minör (küçük) çember yayı denir.
Merkez açının gördüğü yay minör yaydır.
Çemberde minör yayın ölçüsü ile majör yayın ölçüsü toplamı 360º dir.
ÖRNEK : Bir çemberde majör yayın minör yaya oranı 8’dir. Buna göre minör yayı gören merkez açının ölçüsünün kaç derece olduğunu bulalım.
Çözüm
Minör yayın ölçüsünü 1x ile gösterirsek majör yayın ölçüsü 8x olur.
Bu iki yayın ölçüleri toplamı 360º olduğundan; 8x + x = 360º
9x = 360º
x = 40º (minör yayı)
Minör yayının ölçüsü merkez açının ölçüsüne eşit olduğundan, merkez açısı da 40 derecedir.
ÇEMBERDE AÇILAR
1. MERKEZ AÇI
Köşesi çemberin merkezinde ve ölçüsü 0º ve 180º arasında olan açıya merkez açı denir. Merkez açının iç bölgesinde kalan çember parçasına merkez açının gördüğü yay denir.
Merkez açının ölçüsü, gördüğü yayın ölçüsüne eşittir. 
Aynı yayı gören çevre açının ölçüsü, merkez açının ölçüsünün yarısıdır.
ÖRNEK 
Çözüm : Çevre açı ve merkez açı aynı BC yayını görmektedir.
Bu nedenle BAC çevre açısı, BOC merkez açısının yarısıdır.
80 ÷ 2 = 40º dir.
2. ÇEVRE AÇI
Köşesi çember üzerinde olan açıya çevre açı denir. Çevre açının iç bölgesinde kalan çember parçasına çevre açının gördüğü yay denir.
Çevre açının ölçüsü, gördüğü yayın ölçüsünün yarısına eşittir.
Aynı yayı gören çevre açıların ölçüleri eşittir. 
Çapı gören çevre açının ölçüsü 90 derecedir.
Çap çemberi iki eş parçaya böler.
AC yayı = 360º ÷ 2 = 180º
Çevre açı gördüğü yayın yarısına eşittir.
m(ABC) = 180º ÷ 2 = 90º
ÇEMBER PARÇASININ UZUNLUĞU
7. Sınıf Matematik Doğruda Açılar Cevaplı Test 1
7. Sınıf Matematik Çember ve Daire Çözümlü Test
7. Sınıf Matematik Doğruda Açılar Cevaplı Test 2
7. Sınıf Matematik Çokgenler Çözümlü Test